One purpose of the video is to explain how the proof the background independence (an important property of any quantum gravity theory) of string theory is a major success of string field theory. Harold describes which particular problems regarding background independence have been solved using string field theory and which additional progress can be expected in the future. He also discusses how he used machine learning techniques to solve geometrical problems required for constructing string field theory.
Moreover, he talks about his book on String field theory - A modern introduction (Springer, 2020) and how he arrived at writing it.
Congratulations to Harold !

between 1829 and 1907 of the
spatial distributionof cafes
and restaurants in Paris.
Analysis of economic activities during a century of urban growth in Paris Evolution between 1829 and 1907 of the spatial distribution of cafes and restaurants in Paris. Researchers Marc Barthelemy (Institut de Physique Théorique and Centre d'Analyse et de Mathématique Sociales, EHESS), and Julie Gravier (Centre de Recherches Historiques and Centre d'Analyse et de Mathématique Sociales, EHESS) have just published in the prestigious journal Nature cities [1] their findings on the analysis of economic activities in a century of urban growth in the city of Paris.
Contemporary studies on the dynamics of economic activity in growing cities generally focus on periods of a few years or a few decades. Using a recently constructed geohistorical database containing around 1 million entries from historical directories, this study presents a detailed analysis of economic activities in Paris over almost a century (1829-1907).
The authors show that activities can be classified into three categories according to their dynamics and their scaling law in relation to population: (1) linear for everyday needs such as food and healthcare, (2) sublinear for public services such as education and administration, and (3) superlinear for specialized or temporary trends. The study also shows that these activities are highly sensitive to historical events, such as major public works or political conflicts, offering new insights into the evolution of activities in growing cities.
[1] Julie Gravier et Marc Barthelemy, A typology of activities over a century of urban growth, Nature Cities 1, pages 567–575 (2024)
Jorge graduated in Theoretical Physics from the University of Havana (UH), Cuba. He then joined the Center of Molecular Immunology in Havana, a biopharmaceutical institution that develops therapeutic drugs for cancer and autoimmune diseases. He completed his Ph.D. on mathematical models of cellular metabolism in culture, visiting the Beatson Cancer Research Institute (Glasgow, UK) and the Politecnico di Torino (Italy).
Jorge then moved to Paris for a postdoctoral fellowship at ENS, where he worked on the statistical physics of unsupervised representation learning and applications to biological sequences. He was also awarded a PSL Junior Fellowship in Artificial Intelligence. He joins the IPhT on a CNRS "Junior Chair".
Welcome to the IPhT, Jorge!
Next Carlo Heissenberg's arrival at IPhT!
2024-07-18 10:17:00
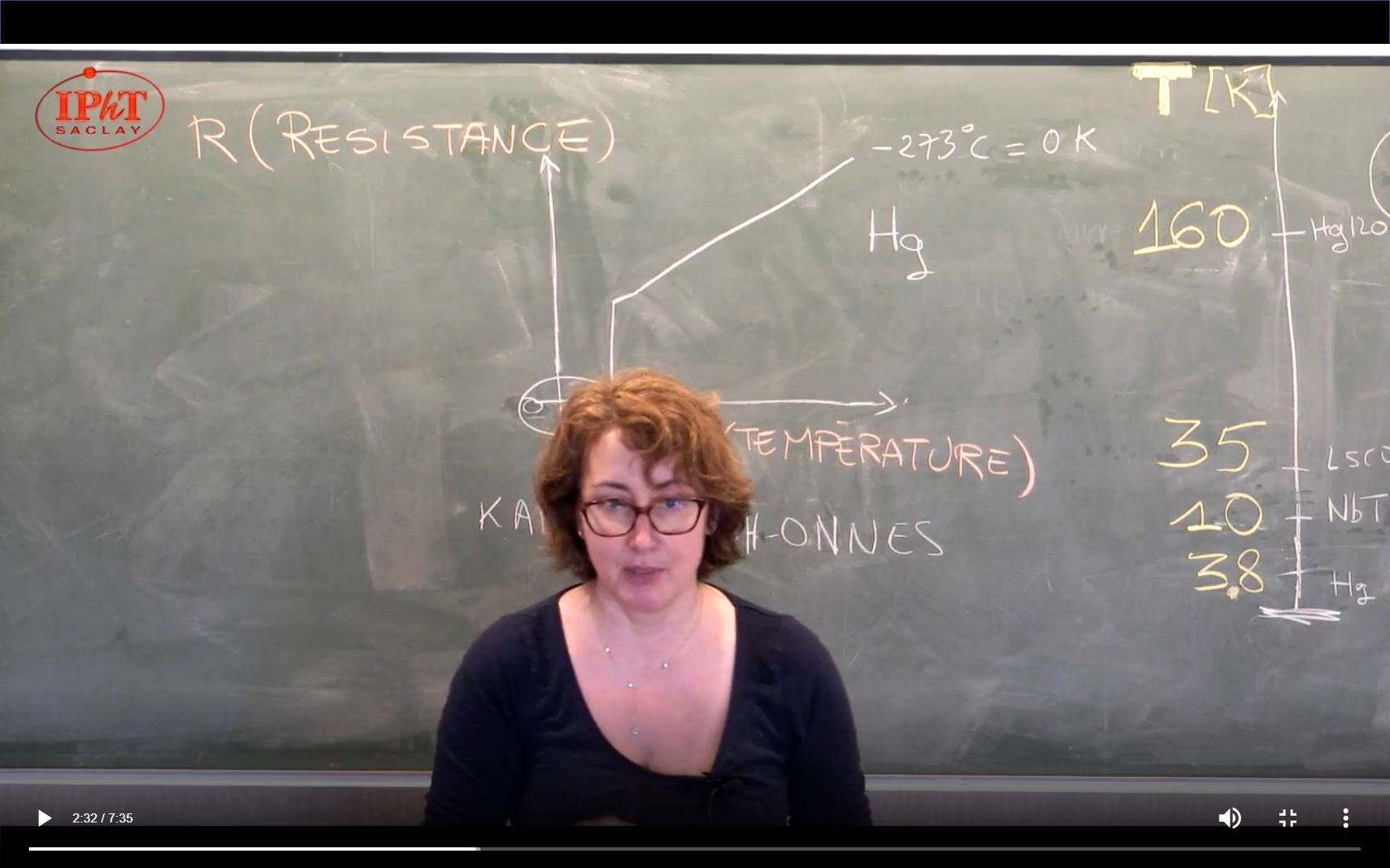
Teaching ideal quantum measurements
2024-07-12 20:18:00
Next arrival of Olivier Gingras at IPhT!
2024-07-05 14:19:00
Supersymmetry Meets Random Matrices
2024-07-04 15:21:00
Dilepton polarization as a signature of plasma anisotropy
2024-06-05 18:52:00
"Les Houches" International School of Physics (July 29- August 23)
2024-05-02 11:21:00
2024-05-02 10:36:00
The Institut de Physique Théorique celebrates Philippe Di Francesco's 60th birthday
2024-04-30 15:31:00
LISA mission gets the go-ahead from ESA
2024-01-26 16:35:00
2024-01-17 15:58:00
A Marc Barthélémy and Vincent Verbavatz's new book: Statistics of Urban populations.
2024-01-11 16:21:00
One IPhT scientist involved in the top 10 breakthroughs of 2023!
2024-01-10 10:55:00
Welcome to Anne Capdepon, Deputy Head of Research Support at the IPhT.
2023-12-14 09:54:00
The first images taken by Euclid revealed
2023-11-17 16:21:00
Celebration of IPHT's 60 years birthday
2023-11-17 15:42:00
A Starting ERC Grant for Ben Wieder
2023-09-06 15:32:00
Death of Michel Gaudin (02/12/1931 -- 04/08/2023)
2023-08-24 09:49:00
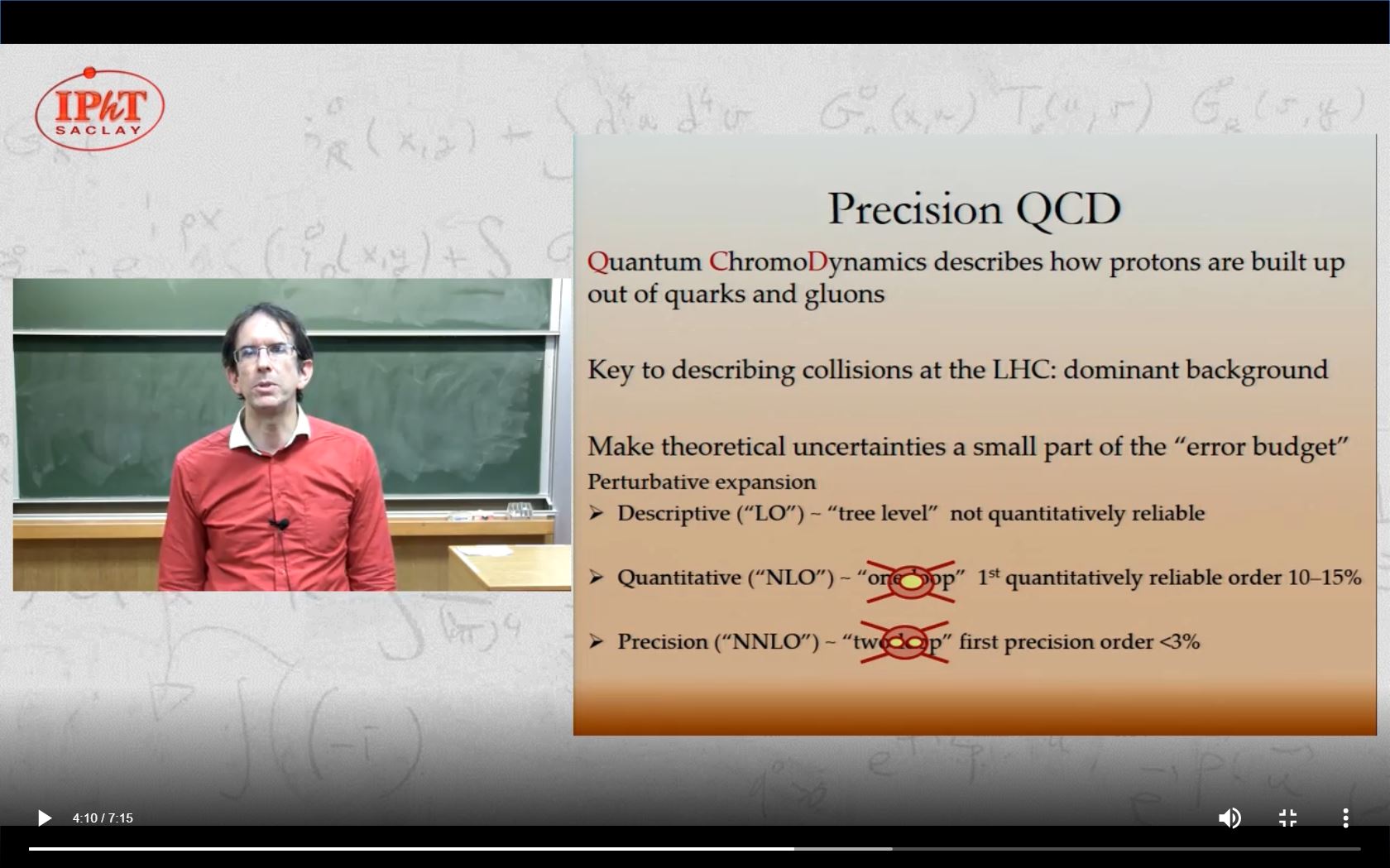
Efficient algorithms for scattering amplitudes
2023-07-12 15:18:00
Matt Von Hippel is to join IPhT on September 1.
2023-05-30 09:40:00
Monica Guica receives the CNRS bronze medal for the year 2023!
2023-04-03 15:21:00
27th Itzykson Conference : Fluctuations far from Equilibrium
2023-03-21 15:39:00
2023 Galileo Galilei Medal for David Kosower (IPhT), Zvi Bern(California U) and Lance Dixon (SLAC)
2023-02-17 09:04:00
Quantum networks : Entangled ions across the university campus Innsbruck
2023-02-10 15:11:00
Hamiltonian paths, a challenge for KPZ.
2023-02-03 15:19:00
Kibble-Zurek phenomenon: from the early Universe to a spin chain
2023-02-03 14:15:00
Kirone Mallick winner of the 2022 Physics French Society (SFP) Paul Langevin Prize
2023-02-01 15:18:00
EPS PhD prize awarded to IPhT student
2022-11-04 10:33:00
Retreat of the IPhT in Autrans : aftermath
2022-06-22 09:05:00
Arrival of Ben Wieder on next september
2022-06-17 15:12:00
Arrival of Dalimil Mazáč at IPhT
2022-06-07 10:14:00
Maps day at IPhT on 24 June 2022
2022-06-03 10:33:00
Quantum bounds and fluctuation-dissipation relations
2022-05-12 11:47:00
26ème conférence Itzykson : "Black-Hole Microstructure IV"
2022-05-12 10:32:00
Colloquium Rencontres de l'IPhT in Autrans (Vercors) from 23 to 25 May.
2022-05-12 10:02:00
An extension of Tutte's formula 60 years later
2022-04-20 11:13:00
2022-04-05 11:28:00
Public talk of Stephane Lavignac on Tuesday March 15th
2022-03-11 09:17:00
A new book written by Marc Barthélémy about spatial networks
2022-02-22 11:05:00
Cédric Villani at IPhT on March 1st
2022-02-22 10:26:00
Summer School in Cargèse around exotic superconductivity
2022-02-07 15:39:00
Langevin Prize of the French Society of Physics for Mariana Graña
2022-02-04 10:46:00
2022-02-01 09:21:00
Maxime Leroy joins the IPHT support team
2022-01-27 15:24:00
Un lien entre la masse du boson de Higgs et la constante cosmologique
2021-11-25 14:11:00
Conférence exceptionnelle de Cédric Villani le lundi 22 novembre à 19h30 (Institut Pascal)
2021-11-18 14:33:00
Mathematical Harmony and the Quantum World
2021-10-07 15:24:00
The art of mathematical physics
2021-09-01 16:31:00
Correlation functions and wave functions in solvable models
2021-08-31 16:44:00
2021-05-01 11:45:00
Multipole Ratios : A New Window into Black Holes
2020-11-27 15:16:00
Orazio Scarlatella lauréat du prix de thèse Physique des Ondes et de la Matière (PhOM) 2020
2020-11-26 11:07:00
Modeling the city: an equation ends centuries-old controversies
2020-11-19 11:10:00
Quantum entanglement: A single photon takes two optical paths by "entangling" them!
2020-10-15 15:06:00
An strongly secured encryption
2020-09-17 17:01:00
Un nouvel ouvrage co-écrit par Pierfrancesco Urbani, physicien à l’IPhT
2020-01-31 14:15:00
Un nouvel ouvrage co-écrit par Henri Orland, physicien à l'IPhT
2020-01-28 16:16:00
Gregory Soyez is the new IPhT Scientist Deputy Director
0000-00-00 00:00:00