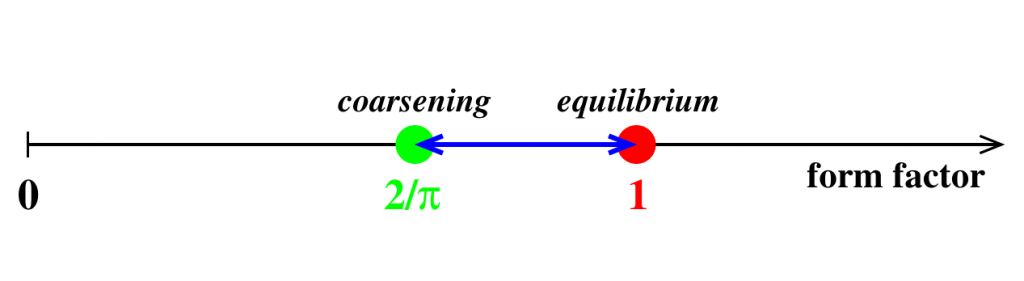
Figure caption: The form factor (dimensionless product of density of domain walls and magnetic susceptibility) provides a novel measure of the distance to thermal equilibrium. Red dot: unit equilibrium value. Green dot: value in zero-temperature coarsening regime. Blue interval: possible range of form factor for everlasting and other kinds of very slow quenches.
What happens when a system is cooled very slowly from its high-temperature phase through a critical point corresponding to a continuous (i.e., second-order) thermal phase transition? This question was addressed in 1976 by Sir Thomas Kibble in the context of the cosmology of the primordial Universe. His goal was to predict the density of relic topological defects (non-trivial field configurations such as monopoles or cosmic strings) that are left behind after the expanding and cooling Universe has undergone one or more continuous phase transitions. Each of these phase transitions lowers the symmetry of fundamental interactions by the spontaneous breaking of the underlying gauge group.
Kibble's approach was extended to statistical physics a few years later by Wojciech Zurek. In both settings, the basic mechanism is that the critical slowing down associated with a continuous phase transition (due to the strong divergence of the relaxation time as the critical point is approached) prevents the cooling system from staying close to thermal equilibrium when it crosses the phase transition. The ensuing heuristic Kibble-Zurek theory predicts scaling laws describing, among other things, how the density of topological defects scales with the cooling rate.
The Kibble-Zurek mechanism has been thoroughly revisited by two permanent members of IPhT, Claude Godrèche and Jean-Marc Luck. In an article entitled “The Glauber-Ising chain under low-temperature protocols”, published recently in the Journal of Physics A: Mathematical and Theoretical, they consider an exactly soluble one-dimensional model, the ferromagnetic chain consisting of classical Ising spins subjected to Glauber dynamics with an arbitrary time-varying temperature. The model has a second-order phase transition at zero temperature. This critical point can be approached along a variety of time-dependent temperature profiles (referred to as quenching scenarios or protocols). However, it cannot be crossed, as negative temperatures are not physically accessible.
The analytical solution of the model becomes significantly simpler in the low-temperature scaling regime, where the relevant spatial and temporal scales are much larger than the microscopic ones, so that many quantities scale as powers of the correlation length of the system. Godrèche and Luck have derived a wealth of analytical results and compared them to the heuristic Kibble-Zurek theory, whenever possible. Two observables characterizing the typical size of the growing ordered spin domains are considered on the same footing, namely the density of domain walls and the magnetic susceptibility. A dimensionless “form factor”, defined as the product of both above observables, is proposed as a novel tool to measure the distance to thermal equilibrium. A paradigmatic situation exhibiting scaling and universality is provided by everlasting quenches, during which temperature approaches zero very slowly. There, as shown in the figure, the form factor varies continuously between two universal values, describing respectively thermal equilibrium and the coarsening regime following an instantaneous quench (i.e., a sudden drop from a very high temperature to zero temperature).
Links to publication:
https://iopscience.iop.org/article/10.1088/1751-8121/aca84c
https://arxiv.org/abs/2208.12512


