La physique statistique et la quantification par intégrale de chemin reposent sur un comptage précis des différents états et configurations d’un système. En particulier, la gravité quantique nécessite l’étude des topologies et géométries possibles de l’espace-temps. Il en résulte des relations profondes entre la physique et la topologie, la combinatoire et la géométrie, ainsi qu’avec la théorie des probabilités. L’IPhT est à l’origine de certaines contributions majeures dans ce domaine et l’Institut compte un certain nombre d’experts dont l’activité couvre un large éventail d’approches.
Dimères, algèbres amassées et au-delà
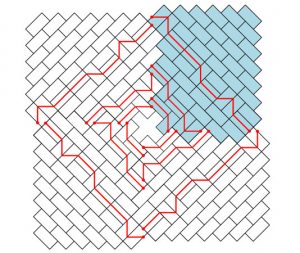

Un problème de pavage symétrique
Modèles de dimères
Les modèles de dimères sont des exemples archétypiques de modèles statistiques ayant de fortes contraintes géométriques sous-jacentes. Ces modèles ont des reformulations naturelles sous forme de pavages de domaines bidimensionnels. Sur des domaines bien choisis et avec des conditions de bord appropriées, de tels pavages donnent lieu à un phénomène de « courbe arctique » où le système présente une séparation nette entre des phases gelées près des bords et des phases fluides loin des bords, un peu comme dans un étang gelé. Plusieurs méthodes ont été utilisées à l’IPhT pour obtenir la forme des courbes arctiques : (1) l’utilisation de solutions exactes des relations de mutation d’algèbre amassée pour les solutions du T-système, qui s’expriment en général comme fonctions de partition de dimères sur des domaines déterminés par les conditions initiales, afin de calculer la densité locale des dimères, dont les singularités déterminent les courbes arctiques ; (2) l’application plus générale de la « méthode de la tangente » qui permet d’accéder à la courbe arctique en calculant des fonctions à un point du bord. Cette dernière méthode a aussi été appliquée avec succès à des modèles de fermions en interaction, tels que les modèles intégrables à 6 vertex et à 20 vertex avec des conditions limites spéciales de type « domain wall ». Des relations remarquables ont également été établies par les chercheurs de l’IPhT entre différents problèmes de combinatoire énumérative, comme par exemple entre le modèle à 20 vertex et le pavage par des dominos d’un domaine convenablement symétrisé.
Algèbres amassées
Les algèbres amassées, inventées au départ comme de pures structures combinatoires, ont trouvé de nombreuses applications en mathématiques (théorie des représentations, géométrie…) et en physique statistique. En bref, une algèbre amassée est un système dynamique « multitemporel » décrivant l’évolution de variables par le biais de mutations. Entre autres contributions, une équipe de l’IPhT a exploré le lien entre la structure de l’algèbre amassée des solutions du T-système satisfait par les matrices de transfert des chaînes de spin quantiques intégrables et la mécanique statistique de modèles de dimères sur certains graphes appelés réseaux. En particulier, les fonctions de partition sur des domaines fixes correspondent à des invariants de mutation. Une structure d’algèbre amassée quantifiée a été utilisée pour calculer les multiplicités des produits tensoriels gradués des représentations apparaissant dans les chaînes de spin quantiques inhomogènes, généralisant l’équation aux différences de Toda. La même structure permet de reformuler la théorie des opérateurs de différence de Macdonald (dont les polynômes de Macdonald sont des fonctions propres communes), en relation avec les symétries des algèbres de Hecke doublement affines sous-jacentes, pour tous les types classiques, ainsi que pour le genre deux.
Une autre activité importante de l’IPhT, à l’intersection de la mécanique statistique, de la géométrie discrète et des systèmes intégrables, consiste à développer des théories qui englobent à la fois des modèles exactement solubles de la mécanique statistique 2d (modèle de dimères, modèle d’Ising, etc.) et des dynamiques intégrables discrètes issues de la géométrie (pentagramme, propagation des Q-réseaux, etc.). Cette activité utilise également des outils de la combinatoire (algèbres amassées, théorie des graphes, etc.).Un autre aspect de la recherche menée à l’Institut concerne la percolation de dernier passage sur le graphe complet et les systèmes de particules en interaction qui y sont liés.
Cartes aléatoires

Les cartes sont des surfaces discrètes composées de polygones collés les uns aux autres. Les cartes aléatoires sont utilisées comme modèle simplifié de la gravité quantique, et leur limite continue est un modèle de surfaces aléatoires en physique statistique. Le problème de l’énumération des surfaces discrètes aléatoires a été résolu dans les cas les plus simples, mais reste un défi pour les surfaces « habillées » avec de la matière (spins d’Ising) ou des couleurs, ou avec une topologie plus complexe, de conditions aux limites non triviales, ou avec des longueurs géodésiques fixes pour certains chemins et, plus généralement, avec plus de structure.
L’approche bijective de l’énumération des cartes
Une technique d’énumération de cartes remarquablement efficace consiste à établir une correspondance bijective entre les cartes planaires et certains types d’arbres généalogiques, appelés mobiles. Initialement limitée aux quadrangulations, cette correspondance a ensuite été étendue à toutes les cartes via la bijection dite BDG (Bouttier Di Francesco Guitter). Ce codage simplifie considérablement l’énumération des cartes et l’approche bijective a finalement permis d’accéder à des résultats d’énumération très fins sur la géométrie aléatoire, tels que le profil des distances qui donne la loi de distribution pour la distance entre deux sommets aléatoires choisis uniformément sur la carte (elle-même aléatoire). Un autre codage bijectif des cartes aléatoires est la « décomposition en tranches », qui consiste à découper les cartes en blocs élémentaires, les « tranches ». Récemment, la décomposition en tranches des cartes planaires à trois bords par les chercheurs de l’IPhT a révélé la profonde analogie qui existe entre l’énumération des cartes et la géométrie hyperbolique.
Cartes et systèmes intégrables
En 2023, une équipe de l’IPhT a prouvé une conjecture de longue date et attendue depuis longtemps par la communauté des combinatoristes, en donnant le nombre de mobiles (qui sont des arbres qui comptent les cartes planaires avec des longueurs géodésiques fixées). La formule coïncide avec la fonction Tau d’un système intégrable hautement dégénéré, et la preuve implique une interaction profonde entre les méthodes des systèmes intégrables et les méthodes combinatoires. En 2021, les chercheurs de l’IPhT ont résolu un modèle combinatoire introduit de manière conjecturale par M. Kontsevich pour la conjecture de Witten sur les r-spins. Les nombres d’intersection R-spin jouent un rôle important en géométrie algébrique et en théorie topologique des cordes. Le problème consiste à compter (mesurer le volume de) l’espace de modules des surfaces de Riemann d’un genre donné et avec des points marqués, dotées d’une structure de r-spin (une forme différentielle fractionnaire dont la puissance r est une 1-forme). Witten avait conjecturé que la fonction génératrice de ces nombres est une fonction Tau r-KdV. Le cas r=2 a été prouvé par M. Kontsevich, qui a décomposé les espaces de modules en cellules étiquetées par des graphes, et a introduit un modèle de cartes aléatoires pour les nombres d’intersection. Pour le cas r-spin, M. Kontsevich a également conjecturé un modèle de graphe. Une équipe de l’Institut a étudié la combinatoire de ces graphes r-spin, et par récurrence sur le nombre d’arêtes, a pu calculer explicitement les fonctions génératrices, montrant qu’elles obéissent d’une part à la récurrence topologique, et d’autre part aux équations r-KdV. En outre, il s’agit d’un magnifique modèle de cartes aléatoires.
Gravité quantique de Liouville, SLE et CLE
Un domaine de recherche intensivement étudié à l’IPhT en collaboration avec des mathématiciens de Cambridge (Royaume-Uni et États-Unis) traite de la géométrie aléatoire conforme des cartes décorées par des modèles de mécanique statistique. Leur limite continue commune doit être décrite par des surfaces aléatoires en gravité quantique de Liouville (LQG), à la fois en tant que mesure et espace métrique aléatoires, et par les chemins aléatoires des évolutions de Schramm-Loewner (SLE) et les ensembles de boucles conformes (CLE). Le couplage naturel entre SLE et LQG et l’utilisation de la relation rigoureuse de Knizhnik-Polyakov-Zamolodchikov (KPZ) donnent une description invariante conforme de cette limite continue. L’approche de la gravité quantique de Liouville par « accouplement d’arbres » a notamment fourni une première preuve rigoureuse que les cartes aléatoires décorées par des amas de Fortuin-Kasteleyn convergent vers des surfaces en LQG décorées par un CLE, dans la topologie dite de la « peanosphère ». Cette approche justifie également l’utilisation de la LQG et de la relation de KPZ pour prédire les formes exactes de tous les spectres multifractals de moyenne intégrale associés aux diverses versions du SLE dans le plan euclidien, ainsi que les fonctions de grandes déviations du CLE.
Modèles de boucles et méandres
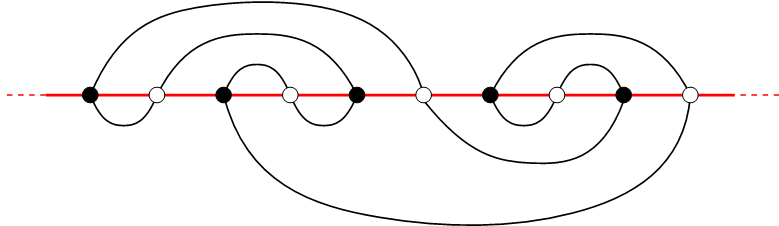
Le problème des méandres est un exemple particulier de modèle de boucles compactes sur des cartes aléatoires, c’est-à-dire des systèmes statistiques de cartes équipées d’un ensemble de boucles qui s’évitent mutuellement et qui visitent tous les sommets de la carte. Cette dernière condition induit de fortes corrélations géométriques entre l’ensemble statistique de boucles et l’ensemble de cartes aléatoires sous-jacentes, ce qui rend la question de l’universalité de ces systèmes beaucoup plus subtile que pour les modèles de boucles habituels. Une direction particulière de l’étude réalisée à l’IPhT consiste à établir une classification des classes d’universalité possibles pour les modèles de boucles compactes et à comprendre les critères pertinents qui font que le système soit dans l’une ou l’autre classe d’universalité. Une attention particulière a également été accordée à la caractérisation des systèmes de boucles par une prédiction de leurs exposants de configuration et de leurs exposants de contact.
Récurrence topologique
La récurrence topologique est une récurrence universelle qui, partant d’une « courbe spectrale » (une courbe algébrique avec une structure supplémentaire), produit une double séquence de formes différentielles Wg,n. Cette récurrence est satisfaite par de nombreux problèmes énumératifs de comptage de surfaces, ainsi que par de nombreuses fonctions de corrélation dans la théorie des matrices aléatoires, les systèmes intégrables et la théorie des cordes. Certaines questions relatives à la récurrence topologique concernent les applications de cette récurrence : prouver qu’un certain modèle (provenant des systèmes intégrables, des matrices aléatoires, de la combinatoire des cartes, de la théorie des cordes, etc.) satisfait à la récurrence topologique, puis l’utiliser pour calculer des fonctions de corrélation. Une autre question concerne la théorie de la récurrence topologique en elle-même : il s’agit alors de prouver certaines propriétés universelles. Une conjecture majeure consiste à prouver que la récurrence topologique fournit le développement WKB des fonctions d’onde des systèmes intégrables : cette conjecture est souvent appelée « conjecture de la courbe quantique ». Elle avait été prouvée dans les cas les plus simples (courbes spectrales rationnelles) et une équipe de l’IPhT l’a prouvée pour les courbes elliptiques, puis les courbes hyperelliptiques, puis les courbes algébriques presque générales.
Triangulations de Delaunay aléatoires

Le modèle des triangulations de Delaunay planaires aléatoires a été proposé par une équipe de l’IPhT en 2013. Il s’agit d’une extension des modèles de cartes aléatoires pour la gravité quantique en deux dimensions, qui possède une invariance conforme explicite au niveau discret. Il est relié aux motifs de cercles, et à de nombreuses structures étudiées dans des contextes proches (combinatoire, cartes et systèmes intégrables, algèbres amassées, géométrie hyperbolique, etc). Des études récentes de l’IPhT (avec l’Université de Brandeis) se concentrent sur la relation entre ce modèle et les déformations des triangulations isoradiales, l’émergence d’un tenseur énergie-impulsion discret, et sa relation avec l’analyticité discrète dans d’autres modèles de mécanique statistique.
Chercheurs permanents
Emmanuel Guitter
Olivier Golinelli
Jérémie Bouttier (en détachement)
Bertrand Duplantier
Sanjay Ramassamy
Bertrand Eynard
Philippe Di Francesco
Dalimil Mazac
Michel Bauer
Hubert Saleur
Sylvain Ribault
Émérites & conseillers scientifiques
André Voros
François David


