Given a set of deformable polygons with prescribed numbers of sides, in how many inequivalent ways can one glue them edge to edge so as to build a sphere? This mathematical question, which pertains to map combinatorics in random geometry, was partially answered by the mathematician William Tutte in a famous 1962 article “A census of slicings” where he solves the problem in the particular case where all the polygons, except at most two of them, have an even number of sides.
In a recent article, Jérémie Bouttier and Emmanuel Guitter (IPhT), in collaboration with the mathematician Grégory Miermont (ENS de Lyon), succeeded, 60 years later, in extending Tutte's formula to the most general case, namely for polygons whose numbers of sides have arbitrary parities. Even though more complex, their general explicit formula is still very elegant and conceals numerous symmetries. It is with no doubt the starting point for new combinatorial discoveries.
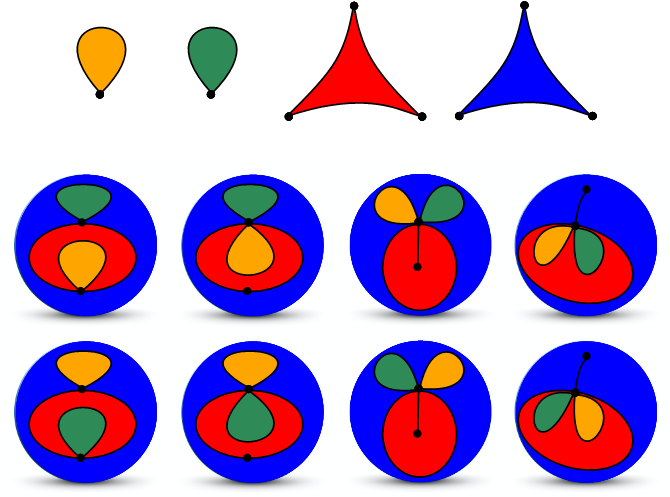
The image shows the 8 ways to assemble two 1-sided and two 3-sided polygons to build a sphere.


