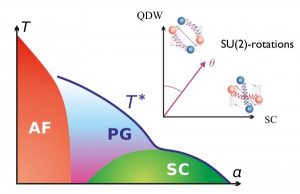
Les sujets étudiés à l’institut comprennent : la supraconductivité dans les matériaux fortement corrélés, la compétition entre la supraconductivité et les phases impliquant une modulation de l’espace réel de la densité électronique, les matériaux bidimensionnels artificiels atomiquement minces, les phases topologiques, les bandes de Chern, la théorie du champ moyen dynamique (DMFT), la chimie quantique topologique, l’effet Hall quantique fractionnaire, les méthodes du groupe de renormalisation de la matrice de densité (DMRG) et le magnétisme quantique.
Chercheurs permanents
Catherine Pépin
Cristina Bena
Benjamin Wieder
Thierry Jolicoeur
Grégoire Misguich