Étant donné un jeu de polygones déformables avec chacun un nombre prescrit de côtés, de combien de façons inéquivalentes peut-on les recoller bords à bords pour fabriquer une sphère ? Cette question mathématique, qui relève de la combinatoire des cartes en géométrie aléatoire, a reçu une réponse partielle par le mathématicien William Tutte dans un article célèbre de 1962 « A census of slicings » où il résout ce problème dans le cas où tous les polygones, sauf au plus deux d’entre eux, ont un nombre pair de côtés.
Dans un article récent, Jérémie Bouttier et Emmanuel Guitter de l’IPhT, avec leur collègue mathématicien Grégory Miermont de l’ENS de Lyon, ont réussi, 60 ans après, à étendre la formule de Tutte au cas le plus général, c’est-à-dire pour des nombres de côtés de parité arbitraire pour tous les polygones. Bien que plus complexe, leur formule générale, tout à fait explicite, reste très élégante et recèle de nombreuses symétries. Elle est sans nul doute le point de départ pour de nouvelles découvertes combinatoires.
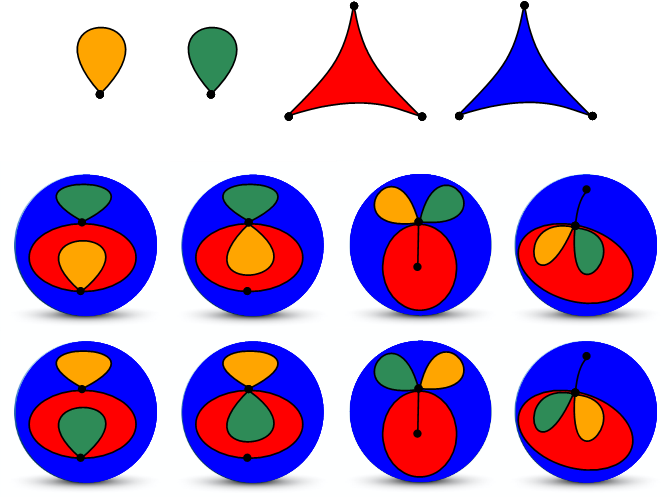
L'image représente les 8 façons d’assembler deux polygones à 1 côté et deux polygones à 3 côtés pour fabriquer une sphère.