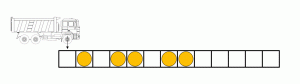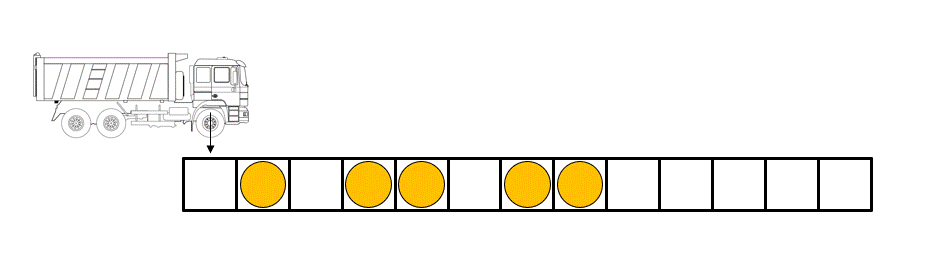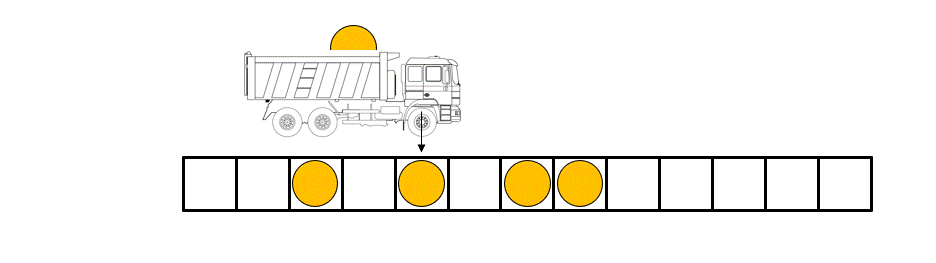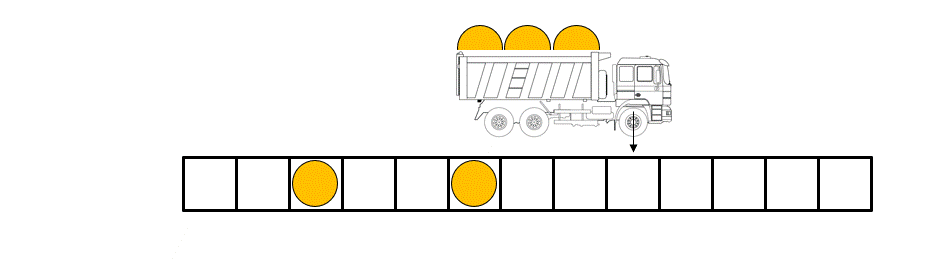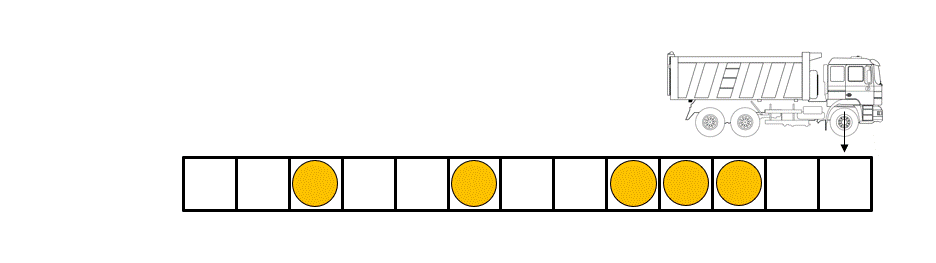
Figure caption: The rules governing the dynamics of the balls in the "box ball system" can be illustrated with the help of a carrier that loads and unloads the balls by running through the system from left to right at each time step.

Understanding how macroscopic laws and large-scale properties emerge from the microscopic interactions between the constituents of a system is a major problem in statistical physics. One can for instance consider the appearance of hydrodynamic behaviors or the way currents react to external forces. It is generally very challenging to connect the microscopic rules to these large-scale properties, and there are relatively few systems for which exact results can be obtained.

The “Box-ball system” (BBS), a particular cellular automaton, is such an example. The BBS consists of “balls” occupying “boxes” arranged on a line, with at most one ball per box. Although the balls move at each time step according to simple deterministic rules (see figure/animation), the BBS presents a rich physics due to the fact that we can identify some objects called "solitons" (a train of k consecutive balls) of all size and whose number are preserved over time.

Using the integrability of the model a recent study of G. Misguich and V. Pasquier, researchers at the IPhT, together with A. Kuniba (Tokyo U.) [1]  has shown how to determine several quantities related to currents and their fluctuations. These include the probability distribution of the number of balls passing through the origin during a time t, the long-time persistent current generated  by a perturbation -- called Drude weight --, and some correlation functions associated with soliton currents.

[1]  “Current correlations, Drude weights and large deviations in a box–ball system”, A. Kuniba, G. Misguich and V. Pasquier, J. Phys. A: Math. Theor., 55 244006 (2022). (https://doi.org/10.1088/1751-8121/ac6d8c) See also J. Phys. A: Math. Theor. 53 404001 (2020). (https://doi.org/10.1088/1751-8121/abadb9)