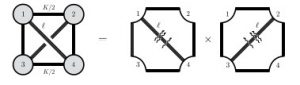
Chaînes de spin intégrables, modèles statistiques sur le réseau et théories des champs intégrables 2d
Les chaînes de spin intégrables sont souvent utilisées comme régularisations sur réseau des théories des champs intégrables. Elles sont particulièrement utiles pour les théories non unitaires ou non compactes, car elles permettent de trouver des solutions analytiques grâce à la théorie des représentations des groupes quantiques. Les théories quantiques des champs non unitaires en 1+1 dimensions apparaissent naturellement dans la description d’une variété de systèmes critiques en mécanique statistique, tels que la percolation et les polymères, ou celle des points critiques quantiques séparant les plateaux dans les isolants topologiques en 2+1 dimensions. L’absence d’unitarité peut être attribuée soit à une non-localité faible, soit au moyennage sur le désordre. Les théories non compactes apparaissent également dans les théories avec désordre, ou dans la description de la gravité quantique à basse dimension. Un effort important est consacré à l’étude des conditions aux limites qui préservent l’intégrabilité et/ou l’invariance conforme. L’intégrabilité est également utilisée pour construire des régularisations sur réseau des défauts topologiques dans les théories des champs conformes à deux dimensions et pour découvrir de nouvelles familles de défauts topologiques. Les modèles intégrables à longue portée sont étudiés pour leur relation avec les théories conformes des champs et pour leurs propriétés mathématiques mettant en œuvre des régularisations sur réseau des algèbres de courants. Le calcul des fonctions de corrélation dans les théories des champs intégrables bénéficie des nouvelles approches de l’Ansatz de Bethe thermodynamique que nous développons.
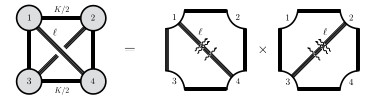
Fonctions de corrélation dans les théories de jauge supersymétriques intégrables à quatre dimensions
Nous nous concentrons sur la limite planaire de la théorie de jauge à supersymétrie maximale à quatre dimensions (MSYM) qui, d’une part, peut être considérée comme un modèle jouet pour la chromodynamique quantique et, d’autre part, est duale à la théorie des cordes dans l’espace Anti-de Sitter. Bien que le problème spectral de cette théorie soit en principe résolu, le calcul des corrélateurs est un défi qui va bien au-delà des techniques d’intégrabilité standard telles que l’Ansatz de Bethe. Nous développons d’autres méthodes, en utilisant la séparation des variables pour les chaînes de spin intégrables, l’approche des facteurs de forme pour les théories des champs 2d intégrables et l’utilisation d’algèbres de symétrie de dimension infinie. Ces techniques ont permis de calculer une fonction de corrélation particulière dans la théorie MSYM pour toute valeur de la constante de couplage. L’objet associé, appelé facteur de forme octogonal, apparaît également dans l’expression de diverses quantités associées à certains modèles super-conformes N = 2. Il est étroitement lié à la célèbre distribution de Tracy-Widom et à sa généralisation à température finie.
D’autres déformations intégrables de la théorie MSYM sont utiles pour calculer les intégrales de Feynman, par exemple la théorie dite « fishnet » (filet de pêche), engendrant des graphes de Feynman rectangulaires. Il a été démontré que les fonctions de corrélation de cette théorie sont invariantes par rapport au Yangien, une algèbre de dimension infinie, et peuvent être déterminées en utilisant les techniques d’intégrabilité et de modèles de matrices.
Chercheurs permanents
| Michel BAUER | |||
| Michel BERGERE | |||
| Jérémie BOUTTIER | |||
| Philippe DI FRANCESCO | |||
| Bertrand EYNARD | |||
| Riccardo GUIDA | |||
| Emmanuel GUITTER | |||
| Ivan KOSTOV | |||
| Grégoire MISGUICH | |||
| Vincent PASQUIER | |||
| Sylvain RIBAULT | |||
| Hubert SALEUR | |||
| Didina SERBAN | |||