Unitarity - which guarantees in particular that the probabilities of all possible events add up to one -
is one of the pillars of quantum mechanics.
In the last few years however, several fundamental problems have seen important new progress thanks to a description in terms of ``non-unitary quantum mechanics". These problems typically involve non-local geometrical aspects, or strong disorder. Two well known examples are percolation, and the model describing the localization/delocalization transition between plateaux in the integer quantum Hall effect. In both cases, the loss of unitarity is the price to pay to use a local field theoretic description for a problem which is initially non local (like percolation), or involves average over disorder.

The loss of unitarity has profound consequences: even if probabilities still add up to one, some probabilities can now be negative, or events whose probability vanishes cannot be discarded any longer. Luckily, these difficulties are compensated by the appearance of super-group symmetries mixing bosonic and fermionic degrees of freedom. For processes involving as many bosons as fermions for instance, probabilities can vanish by a sort of ``boson-fermion compensation", but it does not mean the events are trivial, or can be discarded - they can still intervene as intermediary steps in physical phenomena.

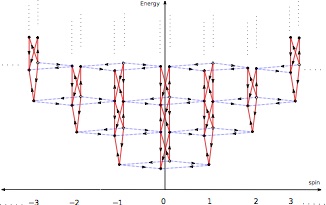
A lot of progress in our understanding of the corresponding field theories (especially in the conformal invariant case) has been realized in the last few years by H. Saleur and collaborators (as part of the Advanced ERC Grant NuQFT). This progress has relied in part - and contributed to - advanced mathematical results in the theory of non semi-simple associative algebras. These algebras describe symmetries where, for instance, some states do not have a definite value of the ``spin''. As a consequence, new physical phenomena appear, like logarithms inside correlation functions of conformal field theories (instead of the pure power laws of the ordinary, unitary case). The figure illustrates the structure of the Hilbert space in a typical non-unitary conformal field theory: dots represent subspaces, and arrows the action of the various symmetry generators. In contrast, a similar figure for an ``ordinary'' unitary conformal field theory would made of simple, non connected, dots.