Dimer models appear in different fields of statistical physics (Ising models), in the theory of correlated electron systems (antiferromagnetic insulators and topological phases of matter), field theory (compactified free field) and combinatorics (partitions and "Aztec diamonds"). These models are built from arrangements of "rods" (dimers) that occupy the bonds of a lattice, and which satisfy a hard-core constrain: each lattice site must touch the end of one and only one dimer. In the quantum versions of these models, the dimers have the possibility to move on the lattice (hopping terms in the hamiltonian), and this leads to some rich quantum many-body models, but which study is in general difficult.

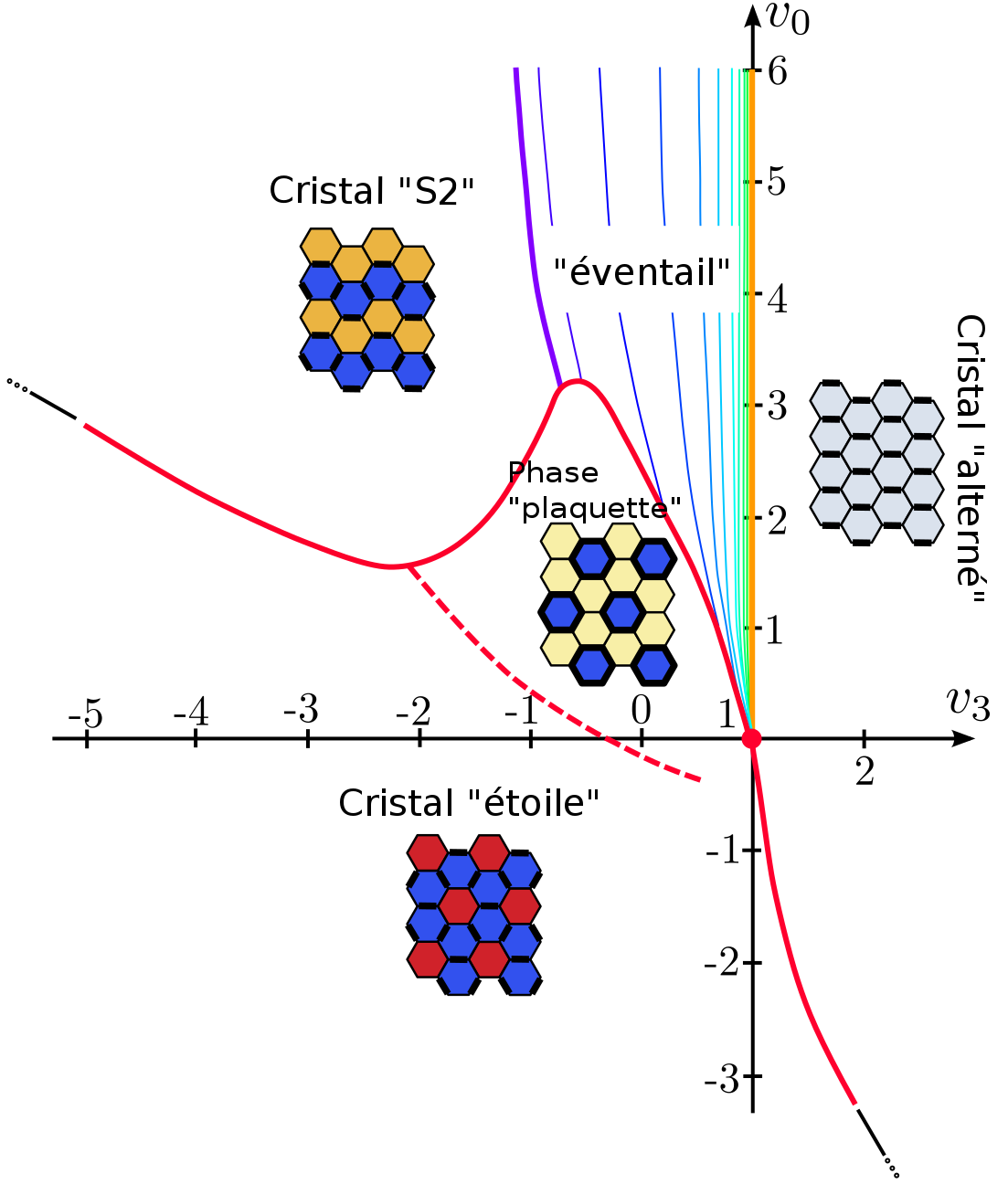
In a recent work [1], some theoreticians (IPhT, Paris-Sud University and P. et M. Curie University) have combined numerical simulations (so-called "quantum Monte-Carlo" methods) and analytical approaches (continuum limit and transfer matrix calculations) to establish the phase diagram of one of these models, on the hexagonal lattice. These results have in particular demonstrated the presence of a "devil's staircase" structure, containing infinitely many commensurate and incommensurate phases, and this has enriched the list of remarkable collective phenomena that can emerge from these geometrically constrained quantum systems.

[1] T. M. Schlittler, T. Barthel, G. Misguich, J. Vidal, et R. Mosseri, Phys. Rev. Lett. 115, 217202 (2015)