 |
Exemples d’exposants mesurés et leur comparaison à KPZ, avant et après renormalisation
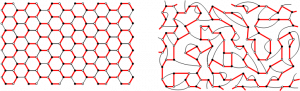
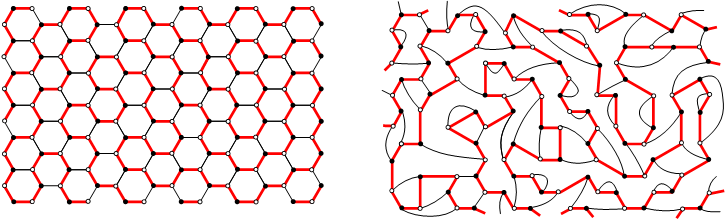
Les chemins hamiltoniens sur réseau, qui sont forcés à visiter sans recoupement tous les sites du réseau, constituent un modèle statistique critique où les contraintes géométriques sont particulièrement fortes. Une équipe de l’IPhT a étudié le cas du réseau en nid-d’abeilles et de son correspondant aléatoire, le réseau bicubique (réseau biparti uniquement fait de vertex trivalents, et colorié en noir et blanc de sorte que les vertex d’une couleur soient reliés uniquement à ceux de l’autre couleur). Les exposants critiques du premier cas sont calculés par la méthode classique dite du gaz de Coulomb, tandis que ceux du second peuvent être obtenus numériquement avec une grande précision à partir du dénombrement exact des configurations de chemins hamiltoniens pour des réseaux de taille finie.
Ô surprise, les relations attendues de KPZ sont mises en défaut pour certains types d’exposants critiques, indiquant qu’un mécanisme nouveau est à l’œuvre qui dépasse leur cadre usuel d’application ! Un procédé (heuristique à ce stade) de renormalisation (réajustement des formules KPZ avec un nouveau paramètre) est proposé qui semble rétablir la validité de ces relations. Le défi consiste maintenant à comprendre mathématiquement comment les contraintes géométriques particulières des chemins hamiltoniens peuvent influencer la statistique du réseau aléatoire biparti, et mener à une telle renormalisation.
Référence : P. Di Francesco, B. Duplantier, O. Golinelli et E. Guitter, Exponents for Hamiltonian paths on random bicubic maps and KPZ arXiv :2210/08887 [math-ph]