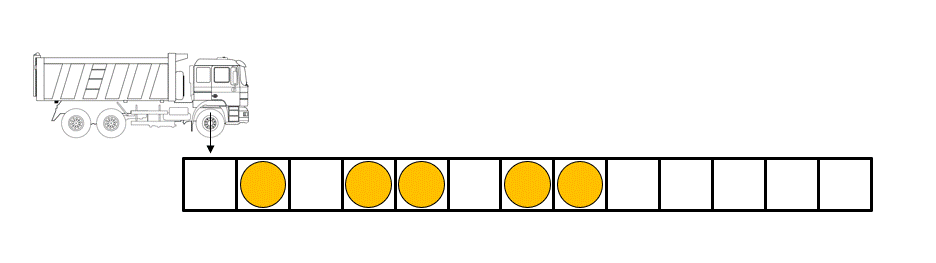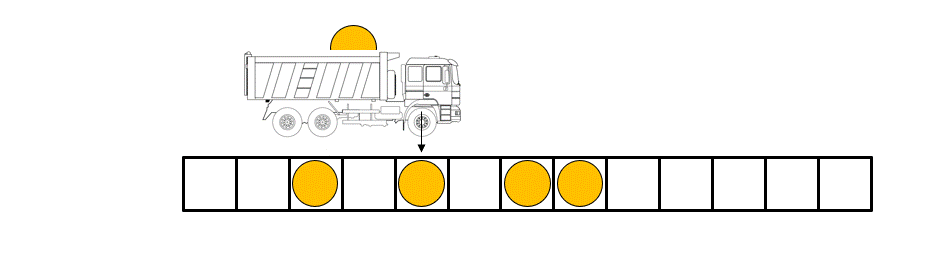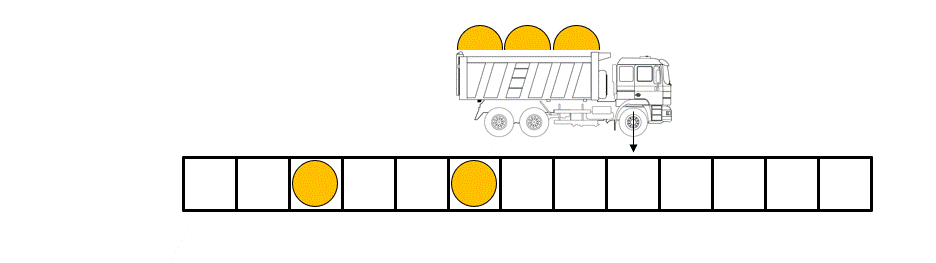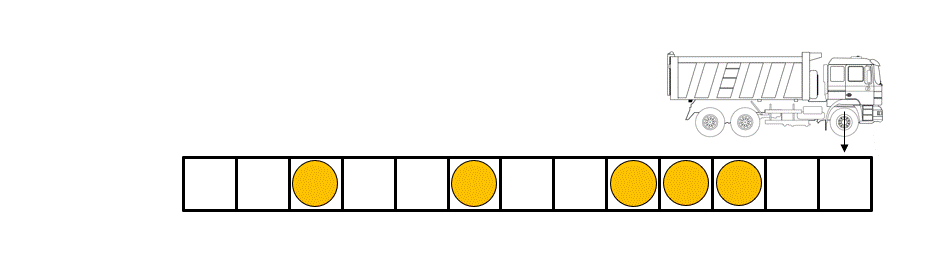
Légende figure : les règles régissant la dynamique des boules dans le « box ball system » peuvent être illustrées à l'aide d'un transporteur qui charge et décharge les boules en parcourant le système de gauche à droite à chaque pas de temps.
Comprendre la façon dont les lois macroscopiques et les propriétés à grande échelle émergent des interactions microscopiques entre les constituants d'un système est un problème fondamental de la physique statistique. On peut par exemple s'intéresser à l'apparition de lois hydrodynamiques ou à la façon dont les courants réagissent aux influences externes. Il est généralement très difficile de relier les propriétés microscopiques aux comportements à grande échelle, et il existe relativement peu de systèmes pour lesquels des résultats exacts peuvent être obtenus.
Le « Box-ball system » (BBS), qui est un cas particulier d'automate cellulaire, en est un exemple. Il se compose de « boules » placées sur des « boîtes » disposées sur une ligne, avec au plus une balle par boîte. Les boules se déplacent à chaque pas de temps selon des règles déterministes simples (voir figure/animation). Le BBS présente une physique riche due au fait que l'on peut identifier des objets appelés « solitons » (un train de k boules successives) de toutes les tailles et dont le nombre reste conservé au cours du temps.
En utilisant l'intégrabilité du modèle une étude récente par G. Misguich et V. Pasquier, chercheurs à l'IPhT, avec A. Kuniba (Univ. de Tokyo) [1] a montré comment déterminer plusieurs quantités liées aux courants et à leurs fluctuations. Parmi ces résultats, on peut citer la distribution de probabilité du nombre de boules traversant l'origine pendant un temps t, le courant rémanent à temps long crée par une perturbation — appelé poids de Drude — , et certaines fonctions de corrélation associées aux courants de soliton.
[1] “Current correlations, Drude weights and large deviations in a box–ball system”, A. Kuniba, G. Misguich and V. Pasquier, J. Phys. A: Math. Theor., 55 244006 (2022). (https://doi.org/10.1088/1751-8121/ac6d8cVoir également J. Phys. A: Math. Theor. 53 404001 (2020). (https://doi.org/10.1088/1751-8121/abadb9)


