La théorie des champs conformes de Liouville est un véritable joyau parmi les théories des champs quantiques en deux dimensions — un exemple rare d’une théorie avec invariance conforme qui est à la fois exactement soluble et fondamentale pour divers sujets de physique théorique. La théorie se base sur de multiples domaines allant de la théorie des cordes et gravité quantique à la géométrie des surfaces de Riemann et même à certains aspects de la théorie des probabilités.
L’une des caractéristiques les plus frappantes de la théorie de Liouville est sa simplicité : grâce à la puissante symétrie sous transformations conformes — quelque chose comme une symétrie sous la transformation « zoom avant » ou « zoom arrière » dans l’espace-temps —, la théorie entière est déterminée par seulement quelques éléments clés :
- un nombre complexe appelé charge centrale noté « c »
- une fonction nommée constante de structure qui encode la façon dont les blocs élémentaires constituant la théorie quantique interagissent. Contrairement à la charge centrale, la constantes de structure n’est pas arbitraire mais doit répondre à des contraintes physiques. Les chercheurs doivent donc la calculer.
Selon la valeur de la charge centrale, les physiciens distinguent deux versions qualitativement différentes (mais étroitement liées) de la théorie de Liouville : la théorie dite spatiale (en anglais: spacelike), correspondant à valeurs de la charge centrale dans le plan complexe avec l’exception de la demi-droite de -infini à 1, et la théorie temporelle (timelike) pour les valeurs de la charge centrale exactement à la demi-droite (-infini,1).
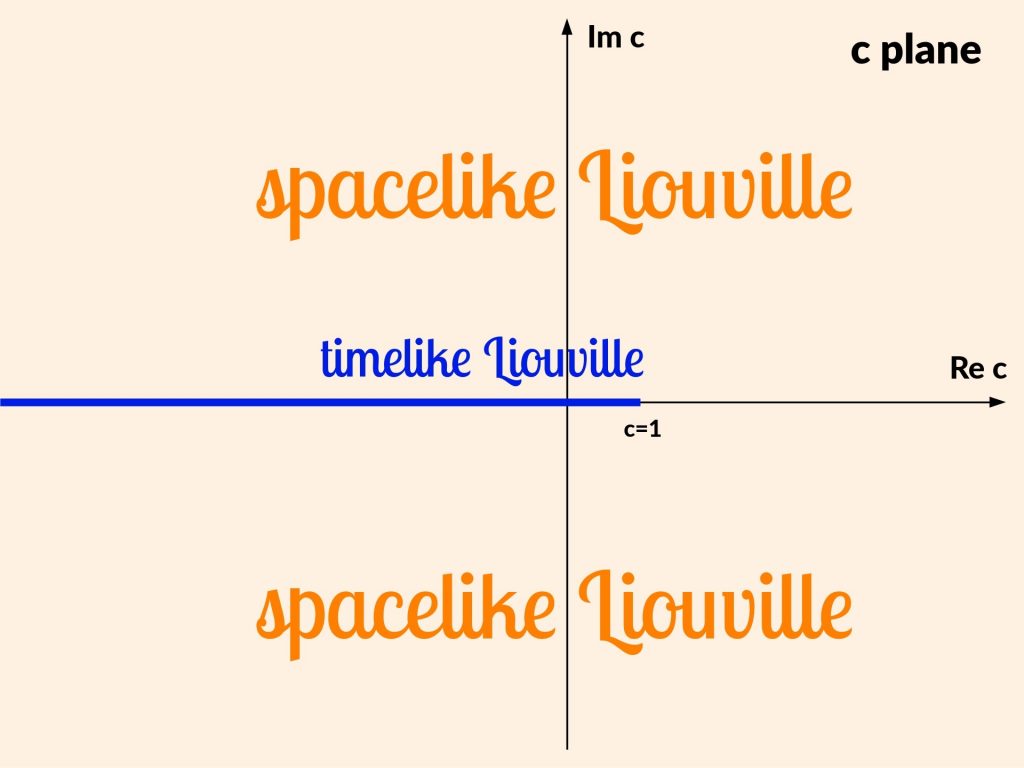
Alors que la théorie de Liouville spatiale trouve des applications dans des domaines tels que la théorie des cordes non critique, la correspondance AdS₃/CFT₂ et l’uniformisation des surfaces de Riemann, la théorie de Liouville temporelle, quant à elle, peut coder des modèles simplifiés de cosmologie, la désintégration d’objets lourds dans la théorie des cordes (appelés D-branes), et trouve même des applications dans des phénomènes critiques bidimensionnels tels que la percolation.
Il existe plusieurs versions de la théorie de Liouville : en plus de la version originale, les physiciens s’intéressent aussi à une extension « supersymétrique » — invariante sous échange fermions / bosons— de cette théorie.
Au cours des dernières décennies, les chercheurs ont fait de grands progrès dans la théorie spatiale, notamment en écrivant les expressions exactes des constantes de structure, que ce soit avec ou sans supersymétrie. Pour la version temporelle sans supersymétrie, les constantes de structure ont été dérivées dans des travaux fondamentaux par d’anciens membres de l’Institut de Physique Théorique (CEA Saclay) (voir https://arxiv.org/abs/hep-th/0306026, https://arxiv.org/pdf/hep-th/0505078). Cependant, le cas temporel avec supersymétrie est resté un mystère ouvert, échappant à une solution complète pendant près de vingt ans.
Dans leur récent travail https://arxiv.org/abs/2505.08890, Beatrix Mühlmann et Vladimir Narovlansky de l’Institute of Advanced Study (Princeton) avec Ioannis Tsiares de l’IPhT ont résolu cette énigme de longue date en dérivant – pour la première fois – les constantes de structure exactes dans la théorie de Liouville avec supersymétrie « N=1 ».
Cette avancée permet non seulement de compléter une partie du puzzle qui manquait depuis longtemps, mais elle ouvre également la voie à de nouvelles applications passionnantes dans le domaine de la gravité quantique, de la théorie des cordes et au-delà !