The gauge/string duality is a half-century old idea, which appeared as an attempt to give an adequate description of strongly correlated quantum field theories, such as QCD. The best studied example of such a duality, known by the name AdS/CFT, is the relation between the maximally supersymmetric multi-color Yang-Mills theory in four dimensions, the conformal invariant  “super-QCD”, and a super-string theory in a ten-dimensional curved space, composed of a 5-dimensional anti-de Sitter (AdS) space and a 5-dimensional sphere.

The dramatic progress of our understanding of AdS/CFT achieved in the last decade was triggered by the discovery that both sides of the correspondence possess the same integrable structure of the type usually associated with two-dimensional systems, as the Heisenberg XXX ferromagnet. AdS/CFT gives the first example of a non-trivial 4-dimensional integrable theory.

In the last years, encouraging results have been obtained for new fundamental quantities, as the gluon scattering amplitudes and the correlation functions at weak coupling, and for the corresponding string-theory objects at strong coupling. These achievements rise hopes that the integrability can be exploited to compute such quantities at any coupling.

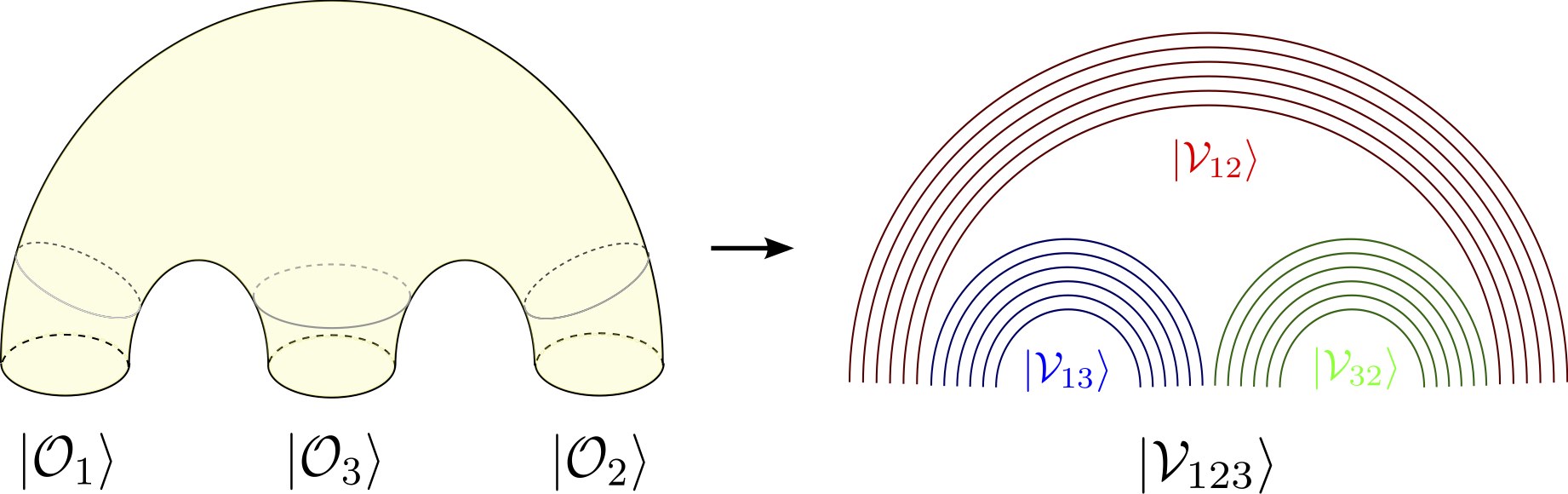
In a recent work [1], a team of IPhT made a step towards reformulating the computation of the three-point function in an integrability-based formalism, without any input from Feynman perturbation theory. This formalism is inspired by the string field theory, which describes the strong coupling limit, but is tailored to work for any coupling. The central object of this formalism is the spin vertex, which is the gauge-theory analogue of the cubic vertex in string field theory. The integrability is manifested by a monodromy condition (Yangian invariance), satisfied by the spin vertex. This condition is expected to define the spin vertex for any coupling and eventually allows to compute the three-point function at any coupling.
[1] Spin Bits and the Spin Vertex, Y. Jiang, I. Kostov, A. Petrovskii and D. Serban, arXiv:1410.8860 (to be submitted to JHEP)