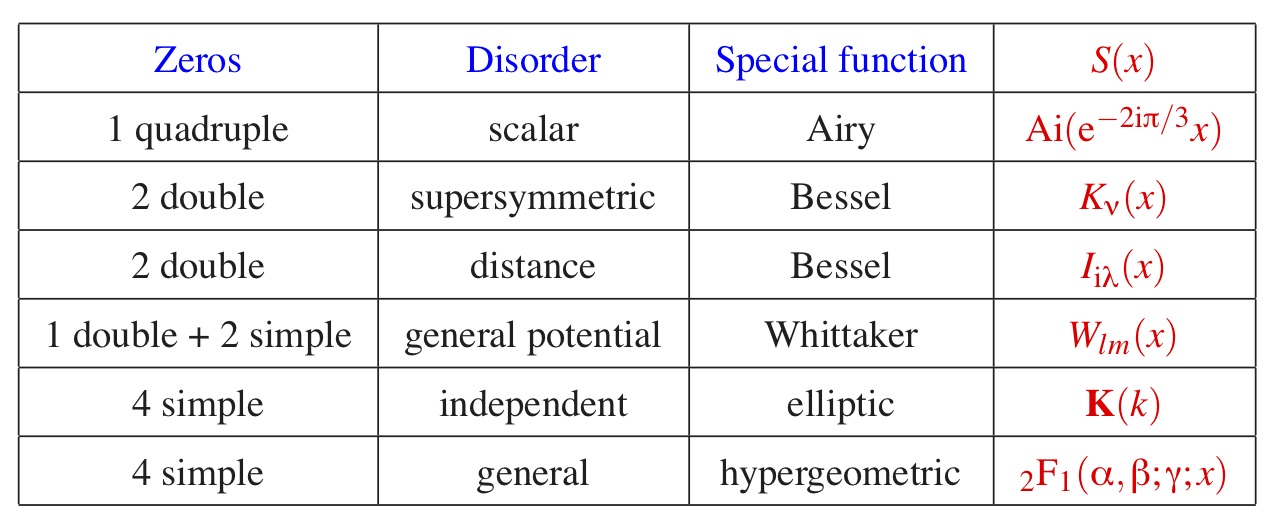
Matrix products provide a natural tool to investigate one-dimensional systems consisting of many units in series, as soon as every unit can be described by means of a transfer matrix. Disordered systems usually yield products of independent random matrices which do not commute among themselves. Many situations of interest are already described by the simplest non-trivial case of 2 times 2 matrices. Typical examples include the Anderson problem of an electron propagating in a random potential, and classical and quantum Ising spin chains with random fields and/or exchange couplings. Furthermore, the most relevant quantities (localization length, density of states, free energy, ground-state energy) can be expressed in terms of the Lyapunov exponent characterizing the exponential growth of the matrix product with the number of factors. Disordered systems of this kind exhibit non-trivial scaling regimes whenever disorder is weak, whilst the system is close to an "interesting" point (band edge for the electron, critical point for the spin chain). In these circumstances the Lyapunov exponent obeys a scaling law as a function of appropriate reduced variables. Jean-Marc Luck and his collaborators have obtained [1] a complete classification of the scaling functions which enter the above scaling laws, within the framework of 2 times 2 real matrices close to the identity. The latter scaling functions are essentially the logarithmic derivatives of the following "special functions": Airy, Bessel, Whittaker, elliptic, hypergeometric (see Table). This list somehow provides a classification of the possible kinds of collective behavior in one-dimensional disordered systems.

[1] Alain Comtet, Jean-Marc Luck, Christophe Texier, Yves Tourigny

The Lyapunov exponent of products of random 2 times 2 matrices close to the identity

Journal of Statistical Physics 150 (2013) 13-65 (arXiv:1208.6430)