Quantum chaos?

Let us consider the quantization of an autonomous Hamiltonian of a closed system (the spectrum is purely discrete).
The evolution in Hilbert space of any initial quantum state is always quasi-periodic (each coefficient of the state in the eigenbasis evolves independently of the others, through a simple rotation). There is no chaos in this linear dynamics.

Quantum chaos (or "chaology") deals with the semiclassical behaviour of quantum quantities, in the case where the classical limit of the Hamiltonian is chaotic, or at least non-integrable.

For a generic Hamiltonian in 2 or more degrees of freedom, one has in general very bad knowledge of the quantum invariants (eigen-values and vectors). The only solvable case is the textbook example of a quantum integrable system, where the Hamiltonian belongs to a family of d commuting operators. The system can then be reduced to a seris of 1-dimensional quantum systems, the spectrum of which can be approximately computed using the Bohr-Sommerfeld-WKB method. This corresponds to solving an ordinary differential equation (which is doable), as opposed solving to a genuine partial differential equation (which is not). 

One of the aims of quantum chaos is to better understand the spectrum (eigenvalues/vectors) of such non-solvable quantum systems, especially in the semiclassical limit, and when the classical limit system is chaotic. Equivalently, it asks the following question:

Where can one detect, in the quantum spectrum, the fact that a system has a classically chaotic limit ?

Quantum maps

In the classical framework, the simplest chaotic conservative systems are maps on 2-dimensional phase spaces, like the 2-torus. Since such a map can be understood as a stroboscopic version of a Hamiltonian flow, it is natural to quantize it into a "quantum propagator", that is a unitary operator on the corresponding Hilbert space. A compact phase space (like the 2-torus) leads to finite-dimensional quantum Hilbert spaces:  the quantized maps are unitary matrices, which can be easily (numerically) diagonalized.
The quantum dimension N is the inverse of Planck's constant h, so the semiclassical limit corresponds to the large-N limit. These matrices have a particular structure (in order to "reproduce" the classical dynamics when N is large). However, when the classical dynamics is chaotic, these matrices share some characteristics with typical NxN unitary matrices (such characteristics are called universal, since they do not depend on the particular dynamics). 

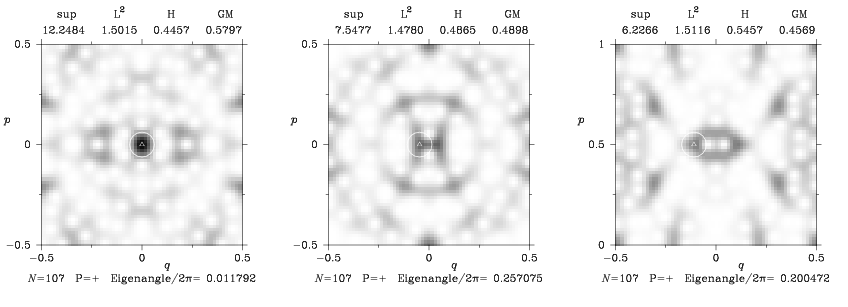
Eigenstates of quantum chaotic maps

To study the semiclassical structure of the eigenstates of such quantum maps, it is convenient to represent these states in phase space, instead of simply as N-dimensional vectors. I focussed on the so-called Bargmann-Husimi representation, which associates to any quantum state a positive function on the torus, called its Husimi density.

Husimi densities of 3 eigenstates of the quantum cat map, for N=107. The left one is the most scarred on the fixed point (0,0), although the second also presents some hyperbolic structure close to that point. (read the article)

The Husimi density of an eigenstate is not rigorously invariant through the classical map.
However, in the semiclassical limit, densities of eigenstates must converge (in some weak sense) to classically invariant measures (Egorov theorem). For an Anosov map like the cat map, there exist plenty of invariant measures, it is natural to ask the following question:

A first answer to this question concerns all ergodic systems (map or Hamiltonian flow), and is called the property of
Quantum Ergodicity (or Schnirelman's theorem). It states that, in the large-N limit, almost all eigenstates will converge to the invariant smooth measure, that is the Liouville measure. 

This convergence does not prevent the Husimi function to strongly fluctuate at small scales (it necessarily vanishes at N points of the torus). Looking at the above plots (especially the left one), we see some enhancement of the Husimi density on the  origin, which is a hyperbolic fixed point of the classical map. Such enhancements, first discovered on eigenstates of chaotic  billiards, are called scars of the periodic orbit. The precise definition of a scarred state is problematic: scarred states still (weakly) converge to the uniform measure; on the other hand, the Husimi density of a random state also fluctuates, but its enhancements can take place anywhere on the torus.

Furthermore, there remains the question of possible exceptional sequences of eigenstates for which the Husimi densities converge to a different measure (e.g. a delta measure on a periodic orbit). A negative answer to that question is called the Quantum Unique Ergodicity  (all eigenstates converge to the Liouville measure). Most people believe that a generic Anosov system satisfies this property.
So far, QUE could not be proven for any system. For the quantized cat map (which possesses very special symmetries due to its linearity), we proved that this property fails: there exist exceptional sequences of eigenstates converging to different invariant measures. If the limit measure contains a delta component on a periodic orbit, the eigenstates are said to be strongly scarred, as opposed to the "weak" scarring described above. On the other hand, not all invariant measures can be semiclassical limits of eigenstates.

Husimi density of a cat eigenstate, strongly scarred on a period-3 periodic orbit (left: linear; right: logarithmic). The density  concentrates on the periodic points, but also on their stable and unstable segments (read the article)

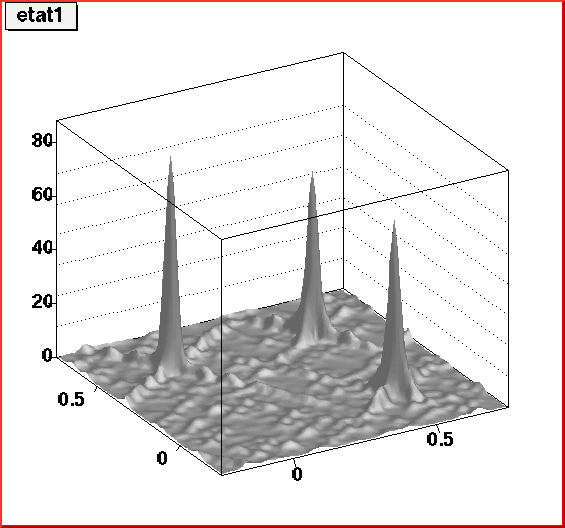
The cat map is not a "generic" Anosov map, due to its linearity. As a consequence, the distribution of its eigenvalues is very different from those of a random unitary matrix (in particular, they can be very degenerate). The strong scarring also seems related with the high degeneracies of the eigenvalues.
For these reasons, it is not at all obvious whether the above results on strong scarring can be extended to nonlinear perturbations of the cat map, which are the generic Anosov maps on the torus.